(22-1)| Début |
Chapitre 2 : Ondes planes |
2-2 : CONDITIONS DE PASSAGE
Il s'agit de déterminer les relations qui lient les composantes des champs de part et d'autre d'un dioptre qui sépare deux milieux caractérisés par :
milieu 1 : 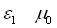(22-1)
milieu 2 :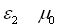 
(22-2)
1- Composantes normales
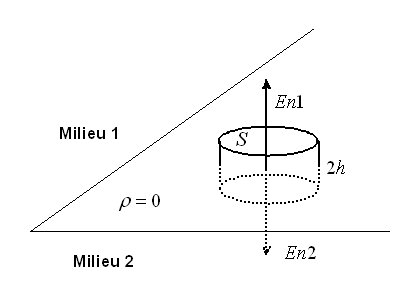
Nous calculons la charge totale contenue à l'intérieur du volume élémentaire du cylindre de surface S et de hauteur 2h soit d'après l'équation (21-6)
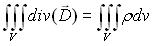(22-3)
comme la charge électrique est supposée nulle, il vient :
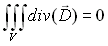(22-4)
En utilisant le théorème d'Ostrogradski, on obtient :
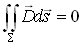(22-5)
Or, le flux de D à travers les parois du cylindre tend vers 0 lorsque la hauteur H du cynlindre tend vers 0, on peut donc écrire :
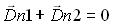soit :
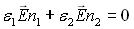(22-6)
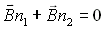soit
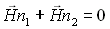(22-7)
1- Composantes tangentielles
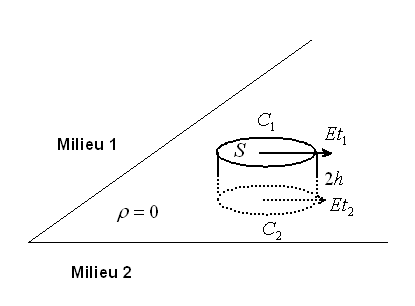
Nous calculons le flux du champ magnétique à travers le cylindre de surface S et de hauteur 2h soit d'après l'équation (21-5)
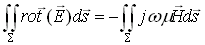(22-8)
D'après la formule de Stockes on peut écrire lorsque la hauteur h tend vers 0 :
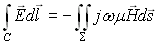(22-8)
Or cette relation doit êtte vraie pour la courbe C1 située au dessus et pour la courbe C2 située dans le milieu 2 ce qui impose que :
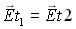et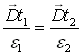 
(22-9)
Le même raisonnement avec l'équation (21-5) conduit à :
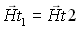et
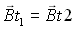(22-10)