2-1 : DEFINITIONS

Un rayon lumineux ne traverse pas deux polariseurs croisés. Ceci n'est possible que si l'onde est transversale à la direction de propagation.

Conclusion : une onde électromagnétique se propageant en espace libre est une onde transversale.

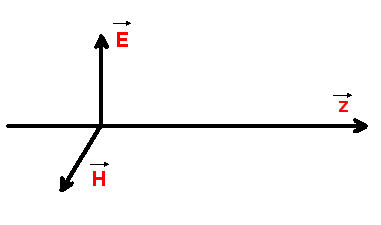
Une onde électromagnétique en propagation libre dans une direction z possède une composante de champ électrique que nous noterons E et une composante de champ magnétique que nous noterons H, E H et z forme un trièdre direct. Le plan contenant E et H est perpandiculaire à la direction de propagation, c'est le plan d'onde.

Hypothèse : Nous considérons dans un premier temps une onde se propageant dans un milieu homogène et infini.

L'onde est caractérisée par :

: la direction de propagation

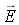: le champ électrique ( en Voltpar mètre) , sa direction indique la polarisation de l'onde

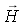: le champ magnétique ( en Ampère par mètre)

Le milieu est caractérisé par :

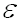- : la permitivité, dans le vide 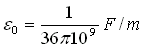s'exprime en Farad par mètre

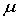- : la perméabilité, dans le vide 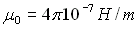s'exprime en Henry par mètre

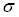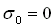- : la conductivité, dans le vide   s'exprime en Mho par mètre ( le Mho est l'inverse de l'Ohm, l'unité de résistance)

Remarque : Dans le cas général, 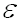,,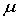 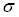sont des tenseurs, dans les milieux homogène et isotropes ce sont des scalaires.

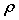- :la densité volumique de charges éléctriques, dans le vide 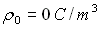s'exprime en Coulomb par mètre cube

A partir de ces grandeurs caractéristiques, il est commode d'introduire :

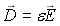- (21-1) l'excitation du champ électrique

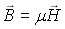- (21-2) l'excitation du champ magnétique

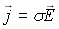- (21-3) la densité de courant, (cette équation n'est autre que la loi d'Ohm)

Toutes ces grandeurs sont reliées par les équations de Maxwell :

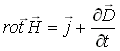(21-4)

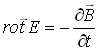(21-5)

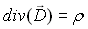(21-6)

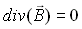(21-7)

Commentaire :

L'équation (4) montre que toutes variations temporelles du champ électrique induit une variation spatiale du champ magnétique, et de même toutes variations temporelles du champ magnétique induit une variation spatiale du champ électrique. Il ne peut donc pas avoir de propagation seule de l'un des champs E ou H, c'est pourquoi l'on parle d'onde électromagnétique.

Remarque 1 : en milieu isotrope, non conducteur 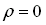(21-8) et pour une onde sinusoïdale ces équations deviennent :

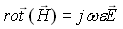(21-9)

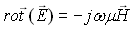(21-10)

(21-11)

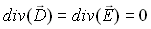(21-12)

Remarque 2 : en milieu isotrope, conducteur 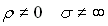(21-13) et pour une onde sinusoïdale ces équations deviennent :

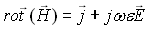(21-14)

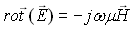(21-15)

(21-16)

 (21-17)

Considérons l'équation 14 dans laquelle nous remplaçons la densité de courant j par sa valeur tirée de l'équation (21-3)

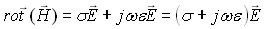(21-18)

Pour obtenir une équation similaire à l'équation (9), nous allons introduire la permittivité complexe sous la forme :

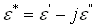(21-19)

et nous allons écrire l'équation 18 sous la forme :

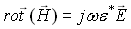(21-20)

qui est similaire à l'équation (21-9), mais pour ce faire il faut que :

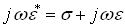(21-21)

soit :

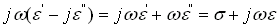(21-22)

de cette relation on tire que :

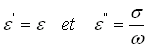(21-23)

Avec les valeurs données par l'expression (23) on pourra facilement calculer les conditions de propagation dans des milieux conducteurs donc avec pertes.