6-2 : ÉQUATION DES TELEGRAPHISTES

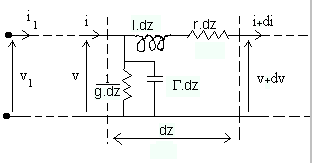
Constantes des lignes : caractéristiques linéiques

Figure 62-1 Grandeurs caractéristiques linéique d'une ligne

r : représente la résistance linéique de la ligne

l : est la self linéique

g : est la conductance linéique

G : est la capacité linéique

Équation des télégraphistes

L'équation des télégraphistes s'obtient en écrivant la loi des mailles et la loi des noeux en régime sinusoïdal ( caractérisé par une pulsation w) pour la quadripôle formé par un tronçon de ligne de longueur dz soit :

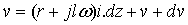(62-1)

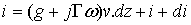(62-2)

nous poserons :

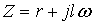(62-3)

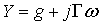(62-4)

ou Z représente l'impédance linéique et Y la conductance linéique de la ligne

Les équations (62-1) et (62-2) deviennent :

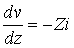(62-5)

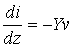(62-6)

ce qui permet d'écrire les équations des télégraphistes :

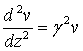(62-7)

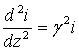(62-8)

en posant :

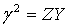
g est la constante de propagation qui s'écrit :

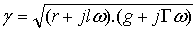(62-9)

Solution de l'équation des télégraphistes

La solution des équations (62-7) et (62-8) est :

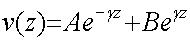(62-10)

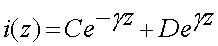(62-11)

En reportant les valeurs des équations (62-10) et (62-11) dans (62-5) et (62-6) on obtient :

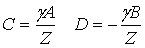(62-12)

Or,

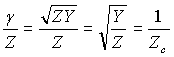(62-13)

Où Zc est homogène à une impédance que nous appelons impédence caractéristique de la ligne, en remplaçant Z et Y par leur valeur tirée de (62-3) et (62-4) on obtient :

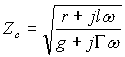(62-14)

En reportant les valeurs données par (62-12) et (62-14) dans les expressions du courant et de la tension, on obtient :

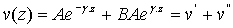  (62-15)

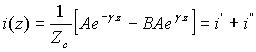(62-16)

Ces deux expressions montrent que deux ondes se propagent sur la ligne :

v' et i' dans les sens des z positifs, c'est une onde incidente

v" et i" dans le sens des z négatifs, c'est une onde réfléchie

Etude de la constante de propagation

De l'expression (62-9) nous déduisons que :

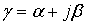(62-17)

de l'expression (62-9) nous tirons :

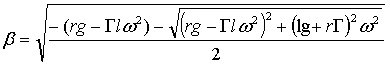(62-18)

qui est la constante de phase

Remarque : nous avons choisi parmi les deux solutions pour b la valeur correspondant au signe - car elle seule conduit à une solution non nulle pour une ligne sans perte comme nous le verrons ci après.

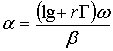(62-19)

qui est la constante d'affaiblissement.

Cas des lignes sans perte

Pour étudier les lignes sans perte, nous allons considérer une ligne de longueur infinie sur laquelle ne se propage qu'une onde incidente qui s'écrit pour la tension :

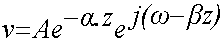(62-20)

L'onde se propagera sans perte si a = 0, ce qui n'est possible que si r et g sont tous deux nuls

Dans ce cas la constante de propagation de simplifie en :

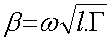(62-21)

Or, nous savons d'après (25-3) que : 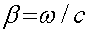en en déduit que :

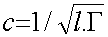(62-22)

Qui représente la vitesse de propagation de l'onde dans une ligne sans perte, elle ne dépend que de l'inductance et de la capacité linéique.

L'expression (62-20) est à rapprocher de l'expression (25-14) que nous avons établie pour les ondes planes en propagation libre.

L'impédance caractéristique

Le rapport tension sur courant à l'entrée d'une ligne de longueur infinie s'écrit :

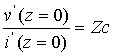(66-23)

On voit donc que l'impédence d'entrée d'une ligne de longueur infinie est égale à l impédance caractéristique de la ligne donnée par l'expression (62-14)

Dans le cas d'une ligne sans perte cette expression devient :

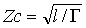(66-24)

Qui alors purement réelle.