Hypothèse : Nous considérons que les ondes se propagent toujours dans la direction z
D'une manière générale, les composantes de l'onde électromagnétique s'écrivent :
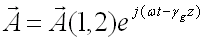 (51-1)
(51-1)
Dans cette expression :
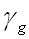 (51-2)
(51-2)
est la constante de propagation
Considérons une zone de l'espace délimitée par un tube supposé parfaitement conducteur de section S conformément à la figure 05-1-1 que nous appèlerons guide d'onde de forme quelconque.
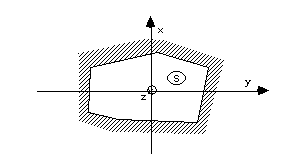
Figure 05-1-1
Montrons qu'une onde Transverse ElectroMagnétique ( onde TEM) ne peut pas se propager dans unguide d'onde.
Une onde TEM n'a pas de composante longitudinale de champ elle se définie donc par :
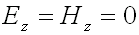 (51-3)
(51-3)
L'équation de Maxwell sur le champ magnétique est :
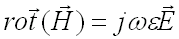 (51-4)
(51-4)
Si nous intégrons cette équation sur un élément de surface S du guide, on obtient :
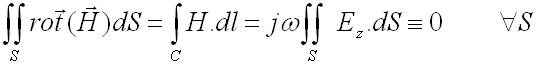 (51-5)
(51-5)
ce qui montre que :
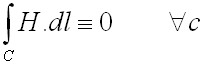 (51-6)
(51-6)
ce qui n'est possible que si :
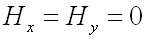 (51-7)
(51-7)
L'équation de Maxwell sur le champ électrique :
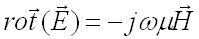 (51-8)
(51-8)
montre que le champ électrique est aussi nul.
Conclusion :
Dans un guide d'onde on ne pas pas propager une onde TEM
Or, l'expérience montre qu'un rayon lumineux peut se propoager au travers du guide d'onde, il existe donc des conditions telles qu'une onde peut se propager dans un guide.
2 - Conditions de propagation d'une onde guidée
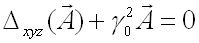 (51-9)
(51-9)E
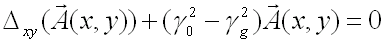 (51-11)
(51-11)
posons :
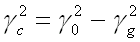 (51-12)
(51-12)
Dans cette expression
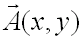 est une quatité réelle donc
est une quatité réelle donc
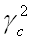 est réelle.
est réelle.
En remplaçant les constantes de propagation par leur valeur en fonction de la longueur d'onde tirées de (51-10) on obtient :
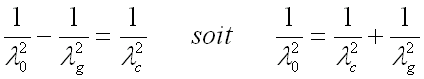 (51-13)
(51-13)
Dans cette expression :
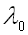 (51-14) représente la longueur d'onde
un milieu infini ayant les propriétés de l'intérieur du guide
(51-14) représente la longueur d'onde
un milieu infini ayant les propriétés de l'intérieur du guide
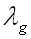 (51-15) représente la longueur
d'onde à l'intérieur du guide
(51-15) représente la longueur
d'onde à l'intérieur du guide
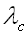 (51-16) represente comme nous le
verrons par la suite une longueur d'onde que nous appelons longueur d'onde de
coupure
(51-16) represente comme nous le
verrons par la suite une longueur d'onde que nous appelons longueur d'onde de
coupure
A partir de la relation (51-13), nous allons considérer deux cas :
1 - La longueur d'onde
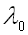 est plus petite que la longueur d'onde
est plus petite que la longueur d'onde
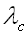 de coupure.
de coupure.
Ceci qui correspond à :
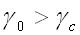 (55-14)
(55-14)
l'expression (51-12) donne :
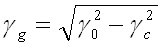 (55-15)
(55-15)
Cette quantité étant réelle, l'onde se propage donc sans perte.
Or,
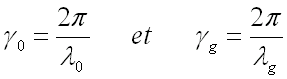 (55-16)
(55-16)
L"expression (51-13) permet de calculer la longueur d'onde guidée :
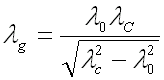 (55-17)
(55-17)
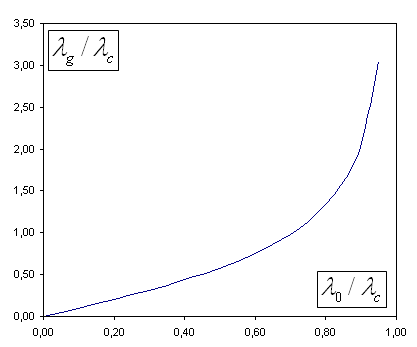
Figure 05-1-2
Remarque :
La longueur d'onde de l'onde guidée ne varie
pas linéairement avec la longueur d'onde
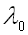 correspondant à la fréquence
du générateur, ce qui donne le diagramme de dispersion.
correspondant à la fréquence
du générateur, ce qui donne le diagramme de dispersion.
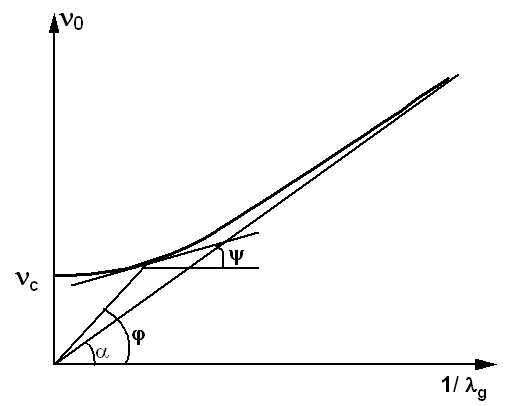
Figure 05-1-3
A partir de ce diagramme, nous pouvons déterminer la vitesse de phase de l'onde guidée
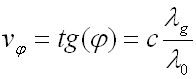 (55-18)
(55-18)
et la vitesse de groupe qui correspond à la vitesse de propagation de l'énergie.
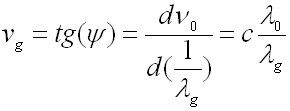 (55-19)
(55-19)
Ces deux vitesses sont reliée par la relation :
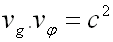 (55-20)
(55-20)
Remarque :
Comme 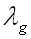 est supérieure à
est supérieure à
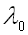 , la vitesse de phase de l'onde guidée est
supérieure à la vitesse de la lumière, ceci n'est pas contradictoire avec les
hypothèses de la relativité car la vitesse de phase ne correspond pas à un
déplacement d'énergie.
, la vitesse de phase de l'onde guidée est
supérieure à la vitesse de la lumière, ceci n'est pas contradictoire avec les
hypothèses de la relativité car la vitesse de phase ne correspond pas à un
déplacement d'énergie.
2 - La longueur d'onde 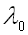 est plus grande
que la longueur d'onde
est plus grande
que la longueur d'onde 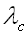 de coupure.
de coupure.
soit 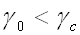 (55-21)
(55-21)
dans ce cas la constante de propagation guidée devient :
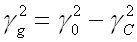 (55-22)
(55-22)
soit
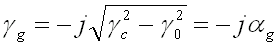 (55-23)
(55-23)
En reportant cette expression dans l'équation de l'onde (51-1), on obtient :
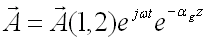 (55-24)
(55-24)
Il s'agit donc d'une onde qui se propage avec une atténuation exponentielle, que l'on nomme onde évanescente.
Conclusion :
Lorsque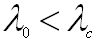 (55-25)
(55-25)L'onde se propage dans le guide sans atténuation ( si le milieu qui rempli le guide est sans perte)
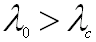 (55-26)
(55-26)L'onde se propage dans le guide avec une atténuation exponentielle.
C'est pourquoi
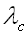 est appelée la longueur d'onde de coupure.
est appelée la longueur d'onde de coupure.