8-3 : LES QUADRIPOLES

Définition

Figure 83-1 Définition du quadripole

Un quadripôle est défini comme un système hyperfréquence possédant un plan d'entré et un plan de sortie, avec des modes de propagation qui peuvent être quelconques.

Coefficient de transfert ( Matrice scattering)

Pour caractériser un quadripôle nous allons définir les grandeurs d'entré et de sortie par rapport aux ondes de référence telles que nous les avons définies au chapitre (8-1).

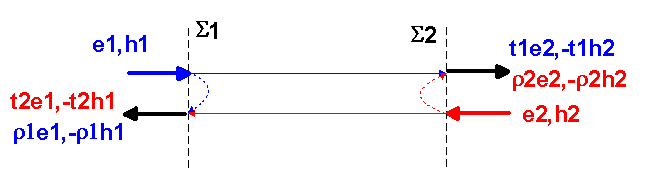
Figure 83-2 : Coefficient caractérisant un quadripôle.

ri sont les coefficients de réflexion (83-01)

ti sont les coefficients de transmission (83-02)

Remarque

L'onde qui sort d'une des entrés du quadripôle provient de l'onde réfléchie à cette entrée et de l'onde transmise de l'autre entrée.

Dans le cas des systèmes linéaires nous pouvons appliquer le principe de superposition pour obtenir :

Figure 83-3 : Composantes caractérisant un quadripôle.

où

les indices ' sont réservés aux ondes incidentes et

les indices " aux ondes réfléchies

ce qui permet d'écrire :

(83-01)

et

(83-02)

Relation entre les coefficients de transmission des systèmes linéaires et isotropes.

Nous allons montrer que seuls trois coefficients sont nécessaires pour caractériser un quadripôle passif linéaire

Nous allons utiliser le théorème de Lorentz.

Démonstration du théorème de Lorentz

Considérons deux régimes de chaps EM caractérisé par ' et ".

nous savons que :

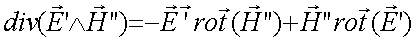(83-03)

Or, d'après les équations de Maxwell, nous avons :

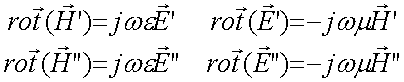(83-04)

 en reprotant (83-04) dans (83-03), il vient :

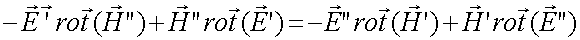(83-05)

ce qui démontre le théorème de Lorentz :

(83-06)

Appliquons le théorème de Lorentz au quadripôle.

Pour cela faisons deux expériences avec la même quadripole:

Expérience ' : la sortie du quadripôle est terminée par une charge adaptée, nous avons le régime de champs suivants :

Figure (83-4) Première expérience

Les champs EM s'écrivent :

(83-07)

Expérience " : la sortie du quadripôle est fermé à l'entrée par une charge adaptée, nous avons le régime de champs suivants :

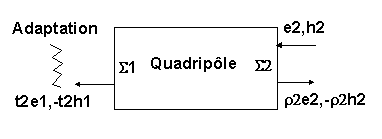
Figure (83-5) seconde expérience

Les champs EM s'écrivent :

(83-08)

Appliquons le théorème de Lorentz qui peut s'écrire :

(83-9)

En appliquant ce théorèpe au surface d'entrée et de sortie du quadripôle on obtient :

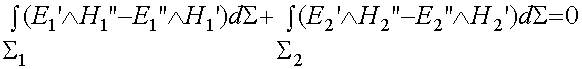(83-10)

En remplaçant dans (83-10) les champs tirés de (83-7) et (83-8) et en remarquant que les ondes de référence sont par définition telles que :

(83-11)

On obtient facilement que :

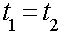(83-12)

Donc, trois coefficients sont nécessaires pour caractériser un quadripôle passif :

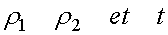(83-13)

remarque :

Pour un quadripôle symétrique nous avons de plus :

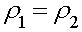(83-13)